Introduction à la modélisation en épidémiologie : COVID-19 - 2ème flambée

Claire Gillier, Clara Gueguen, Sarah Lejosne, Louise Malot (M1 Agro Rennes), le 17 mars 2021.

Edité par Frédéric Hamelin et Marine Dorand (M1 MODE), le 12 mai 2021.

Dans le cadre du projet de modélisation, nous avons travaillé sur la deuxième flambée de l’épidémie de COVID19 en France. C’est-à-dire sur la période s'étalant du 1er Septembre 2020 au 31 octobre 2020. Ce travail présente l’ajustement du modèle SIR utilisé dans l’étude des épidémies. Nous avons travaillé avec R.

Modèle épidémiologique

Le modèle SIR est composé de 3 compartiments $S$ , $I$ et $R$ . On les définit de cette façon :

$S(t)$ : les individus susceptibles d’être infectés à la date $t$
$I(t)$ : les individus infectés à la date $t$
$R(t)$ : les individus remis à la date $t$

Le modèle SIR a pour équations: $\begin{eqnarray*} \frac{\mathrm{d} S(t)}{\mathrm{d} t}&=& -\frac{\beta}{N} S(t)I(t)\,,\\ \frac{\mathrm{d} I(t)}{\mathrm{d} t}&=& \frac{\beta}{N}S(t)I(t) - \gamma I(t)\,,\\ \frac{\mathrm{d} R(t)}{\mathrm{d} t}&=& \gamma I(t)\,. \end{eqnarray*}$ avec les paramètres suivants :

$N$ : la taille de la population
$\gamma$ : le taux de guérison
$\beta$ : le taux d’infection

Ce sont des "taux" par unité de temps.

Modèle d'observation

L'ajustement du modèle se fera par maximisation de la vraisemblance (likelihood en anglais). Cette méthode consiste à maximiser la probabilité des observations sachant les paramètres. Le modèle d'observation définit la probabilité qu'un test soit positif au temps $t$ d'après le modèle épidémiologique : $p(t)=\frac{\sigma I(t)}{I(t)+\kappa S(t)}\,,$ où $\sigma $ est la sensibilité des tests PCR (supposée connue) et $\kappa$ est probabilité relative pour les individus sensibles de se faire tester comparativement aux infectés (à estimer). Aussi, le nombre de tests positifs le jour $t$ peut être modélisé comme un tirage dans une loi Binomiale de paramètres $p(t)$ et $n(t)$ (le nombre de tests réalisés le jour $t$ ) : le nombre de nouveaux cas observés le jour $t$ est $c(t)\sim \mbox{Binomial}(n(t),p(t))$ En admettant que les observations sont indépendantes conditionnellement au modèle, la vraisemblance s'écrit : $\mbox{Like}(\theta)=\prod_{t=0}^{T} \mbox{Prob}(\mbox{observe }c(t)|\mbox{ model predicts }p(t))\,.$ Soit $\theta = \{ \beta, \kappa \}$ le vecteur des paramètres à estimer. Rechercher les valeurs de $\theta$ qui maximisent la vraisemblance est équivalent à rechercher les valeurs de $\theta$ qui maximisent la log-vraisemblance, qui transforme le produit en somme : $\mbox{logLike}(\theta)=\log(\mbox{Like}(\theta))=\sum_{t=0}^T \log\left (\mbox{Prob}(\mbox{observe }c(t)|\mbox{ model predicts } p(t) )\right)\,.$ Nous travaillerons avec la log-vraisemblance.

Traitement des données

Dans un premier temps, on s’assure que l’environnement de travail est vide. Les commandes suivantes effacent les variables ainsi que les fenêtres créées lors des exécutions précédentes.

rm(list=ls()) 
graphics.off()

Installation et chargement des packages :

library(dplyr) # Permet de manipuler les données
library(deSolve) # Permet de résoudre des équations différentielles ordinaires (EDO)

Le package deSolve sera utilisé pour simuler le modèle SIR.

Importation des données

Les données de tests ont été téléchargées depuis le site suivant : Données relatives aux résultats des tests virologiques COVID-19 | SI-DEP.

La commande read.csv2 permet d’importer un ficher csv de données dans R. Il faut préciser si la première ligne header correspond aux noms de colonnes et quel est le séparateur sep des données.

urldata = url("https://www.data.gouv.fr/fr/datasets/r/dd0de5d9-b5a5-4503-930a-7b08dc0adc7c")
data1 = read.csv2(urldata, header=TRUE, sep=";")

Les commandes select et filter permettent ensuite de sélectionner les colonnes souhaitées du tableau de données et les valeurs. Dans le tableau de données, on sélectionne les colonnes jour pour les dates des tests, la colonne P correspond au nombre de tests positifs et la colonne test T correspond au nombre de tests totaux. Les lignes cl_age90 =0 indiquent les lignes où se trouvent les sommes des tests positifs (colonne P) et la somme des tests réalisés (colonne T) au jour t pour chaque jour et tout âge confondu.

data2<-data1 %>% 
  select(jour,P,T,cl_age90) %>% 
  filter(cl_age90=="0")

Ensuite, on sélectionne la période sur laquelle on souhaite travailler. On sélectionne la période du 1er septembre 2020 au 31 octobre 2020 dans le but de modéliser uniquement la flambée (qui sera suivie par un confinement).

data<-filter(data2, jour>= "2020-09-01",jour<= "2020-10-31"  ) # Sélection des dates

PT=as.integer(as.character(data[,2])) # Tests positifs
TT=as.integer(as.character(data[,3])) # Test totaux

LP=length(PT) # Permet de connaître la longueur du vecteur et donc de savoir combien de jours constituent la période de la deuxième flambée
LT=length(TT)

Visualisation des données

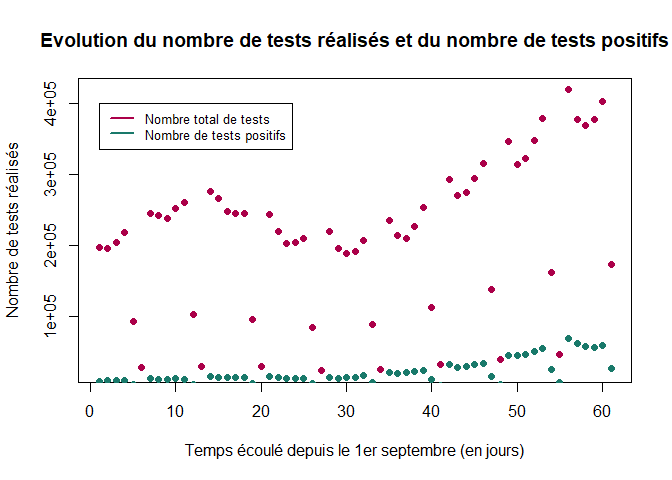
Les graphiques suivants représentent l’évolution du nombre de tests (réalisés ou positifs) au cours du temps.

plot(1:LT,TT,xlab="Temps écoulé depuis le 1er septembre (en jours)",ylab="Nombre de tests réalisés",col="#AB0049",pch=16, main="Evolution du nombre de tests réalisés et du nombre de tests positifs")

points(1:LP,PT,xlab="Temps écoulé depuis le 1er septembre (en jours)",ylab="Nombre de tests positifs",col="#19796A",pch=16)

legend(1, 4e+05, c("Nombre total de tests", "Nombre de tests positifs"),col=c("#AB0049", "#19796A"), lty=1, cex = 0.8,lwd=2)

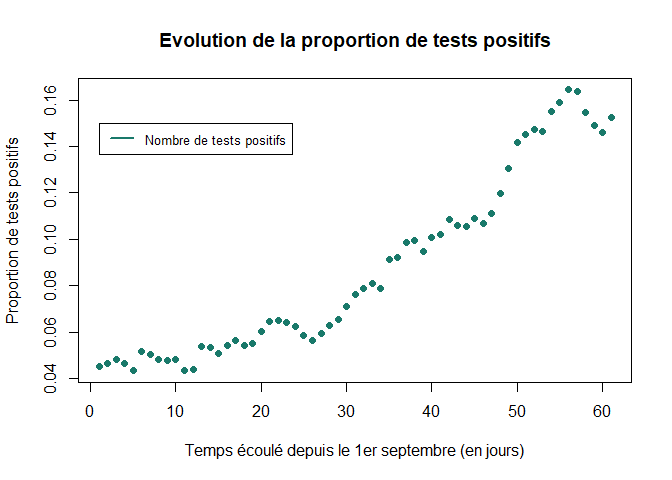
Le graphique suivant montre l’évolution de la proportion de test positifs dans le temps. On calcule PP qui correspond à la proportion de tests positifs observés.

PP=PT/TT 

plot(1:LP,PP,xlab="Temps écoulé depuis le 1er septembre (en jours)",ylab="Proportion de tests positifs",col="#19796A", pch=16, main="Evolution de la proportion de tests positifs")
legend(1, 0.15,c("Nombre de tests positifs"),col=c("#19796A"), lty=1, cex = 0.8, lwd=2)

Ajustement du modèle aux données

Initialisation du modèle

Valeurs initiales des paramètres :

N=67e6 # Taille de la population française
gamma=1/10 # Taux de guérison (inverse du temps moyen avant guérison)
R_0=3 # Reproductivité du virus
beta = gamma*R_0 # Taux de transmission du virus 
sigma = 0.7 # Sensibilité des tests
kappa = 5e-3 # Biais d'observation

En $t = t_0$ , les conditions initiales pour le modèle SIR sont les suivantes :

$I_0 = I (t_0)$ : le nombre de personnes infectées à $t= t_0$
$R_0 = R(t_0) = 5\% \times N$ : nombre d’individus remis au début de la flambée
$S(t_0) = N − I_0 − R_0$ : nombre d’individus susceptibles d’être infectés

On initialise également :

$X_0 = \{ S_0, I_0 \}$ : vecteur d’état
$P_0 = \{ \beta , \kappa \}$ : vecteur des paramètres à estimer

Les conditions initiales sont :

t0 = 1 # Date de départ de la 2ème flamblée : le 1er septembre
I0 = 100000 # Nombre de personnes infectieuses le 1er septembre (estimation grossière)
R0 = (5/100)*N # Nombre de personnes immunisées au 1er septembre (estimation grossière) 
S0 = N-I0-R0 # Nombre de personnes susceptible d'être infectées 
X0 = c(S0,I0) # Vecteur d'état
P0=c(beta,kappa) # Vecteur des paramètres a estimer
t=t0:LT # Vecteur temps

Il est difficile de trouver une estimation précise de $I_0$ . Au 1er Septembre 2020, le nombre d’individus infectés et hospitalisés est d’environ 22 000, ce qui nous permet de prendre un $I_0$ élevé. Après différents essais, il apparaît que quel que soit $I_0$ appartenant à un large intervalle, l'ajustement du modèle est inchangé. Cet exercice ne permet pas d'estimer $I_0$ . On a donc fixé $I_0$ a $100 000$ individus. De la même façon, nous avons donné une valeur arbitraire mais raisonnable à $R_0$ .

Création d’une fonction SIR de façon à simuler le modèle SIR avec la fonction ode plus tard. La fonction ode est une fonction prédéfinie dans R qui permet de résoudre des équations différentielles ordinaires.

SIR = function(t, X, P){ 
  beta=P[1]
  S=X[1]
  I=X[2]
  y=beta*S*I/N # Nombre de nouvelles infections/jour
  dS = -y
  dI = +y - gamma*I
  dX=c(dS,dI)
  return(list(dX))
}

Fonction de Vraisemblance

La fonction logLike est une fonction qui calcule la vraisemblance des paramètres $\beta$ et $\gamma$ d'après le modèle :

logLike=function(theta){ 
  P=theta[1:2] # Vecteur des paramètres à estimer
  beta=P[1] 
  kappa=P[2]
  S0=N-I0-R0
  X0=c(S0,I0)
  X=ode(X0,t,SIR,P) # La fonction "ode" permet de résoudre des équations différentielles

  p=sigma*X[,3]/(X[,3]+kappa*X[,2]) # Probabilité qu'un test soit positif 
  L=dbinom(PT, TT, p, log=TRUE) # dbinom = distribution binomiale
  LL=sum(L) # Log-vraisemblance
  return(LL)
}

Avec p la proportion théorique des tests quotidiens positifs et L la probabilité d’observer un nombre de tests positifs sachant le nombre total de tests réalisés.

Maximisation de la vraisemblance

La fonction d’optimisation optim est une fonction prédéfinie par R. Elle prend en arguments d'entrée les valeurs initiales des paramètres passés en arguments dans la fonction logLike, la fonction logLike elle-même ainsi qu’un troisième argument : control=list(fnscale=-1). Ce 3ème argument sert à maximiser la quantité à optimiser qui, par défaut, est minimisée. Nous appelons opt le résultat de l'optimisation.

opt=optim(P0,logLike,control=list(fnscale=-1)) 

# Paramètres optimisés
beta=opt$par[1]
kappa=opt$par[2]

Les valeurs des paramètres optimisés (qui maximisent la vraisemblance) sont les suivantes :

$\beta \approx 0.13$ : taux d’infection
$\kappa \approx 0.02$ : probabilité qu’une personne sensible se fasse tester relative à une personne infectée

Dynamique épidémique avec les paramètres optimisés

On simule à nouveau la dynamique épidémique avec les paramètres optimisés ci-dessus à l’aide de la fonction prédéfinie ode. Ensuite, on calcule $p$ : la proportion théorique de tests quotidiens positifs.

X=ode(X0,t,SIR,beta)
p=sigma*X[,3]/(X[,3]+kappa*X[,2])

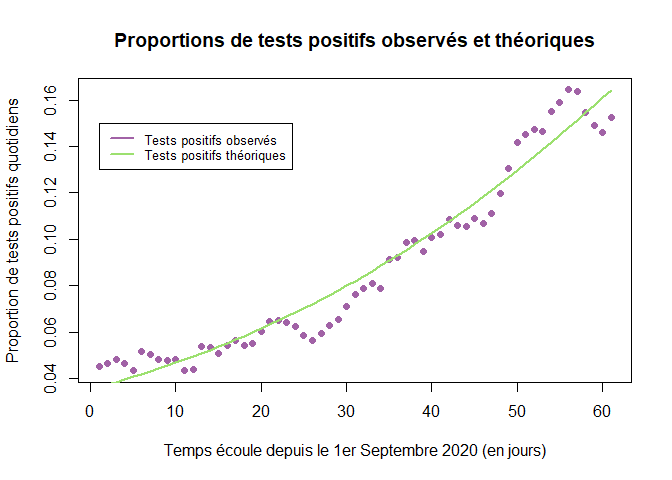
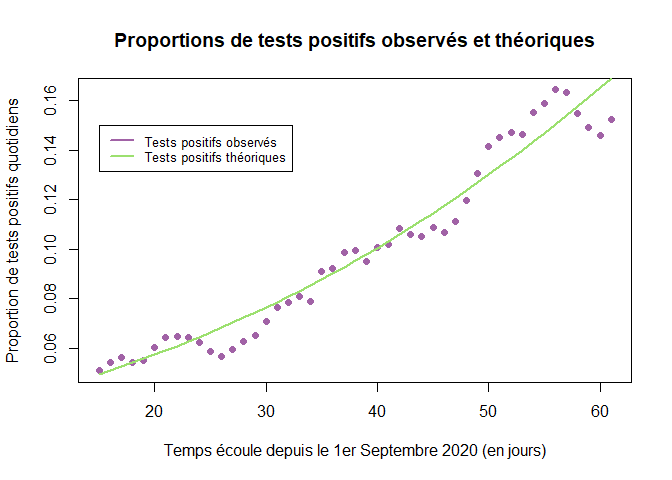
On réalise ensuite un graphe représentant l’évolution de la proportion de tests positifs observés, PP, et de la proportion théorique de tests positifs calculés, p.

plot(t,PP[t],pch=16,col="#A162A6", 
     xlab="Temps écoule depuis le 1er Septembre 2020 (en jours)",
     ylab="Proportion de tests positifs quotidiens",
     main="Proportions de tests positifs observés et théoriques")
lines(t,p, lwd=2, col="#9CE06F")
legend(1, 0.15, legend=c("Tests positifs observés", "Tests positifs théoriques"),col=c("#A162A6", "#9CE06F"), lty=1, cex = 0.8,lwd=2)

Puis on compare $\sigma_1$ (somme cumulée des tests positifs observés) avec $\sigma_2$ (somme cumulée des tests positifs observés). On fait ensuite un graphique des sommes cumulées (cumsum) des tests positifs théoriques et observés.

sigma1=cumsum(PT[t])
#nombre total de tests réalisés * proportion de tests positifs théoriques
sigma2=cumsum(TT[t]*p) 
plot(t,sigma1,pch=16,xlab="Temps écoule depuis le 1er septembre 2020 (en jours)",ylab="Somme cumulée des tests positifs",col="#A162A6", main = "Comparaison des sommes cumulées des tests positifs")
lines(t,sigma2,lwd=2, col = "#9CE06F" )
legend(1, 900000, legend=c("Tests positifs observés", "Tests positifs théoriques"),
       col=c("#A162A6", "#9CE06F"), lty=1, cex = 0.8, lwd=2)

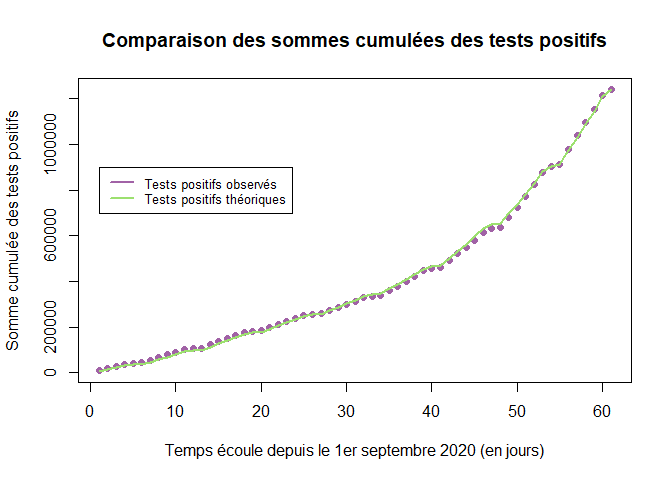
En réalisant un graphique des sommes cumulées des tests positifs théoriques et des tests positifs observés, on peut vérifier que l'ajustement du modèle aux données semble très bon.

Estimation de la Reproductivité du virus

Le modèle est bien ajusté et optimisé aux données épidémiologiques. Cependant, ce modèle ne prend pas en compte les décès. L’ajout d’un compartiment décès au modèle permettrait d'estimer le taux de létalité du virus lors de la deuxième flambée. On peut néanmoins estimer la reproductivité du virus : $\mathcal R_e = \frac{\beta}{\gamma}\frac{S(t_0)}{N}\,.$

R_e1 = (beta/gamma)*(S0/N)
print(paste("R_e=",R_e1))

On trouve une reproductivité $\mathcal R_e \approx 1.30$ .

Pour aller plus loin : prise en compte des décès

Cette extension a été réalisée par Marine Dorand dans le cadre d'un stage de M1 MODE en avril-mai 2021.

Modèle épidémiologique

On considère maintenant un modèle de type SIRD :

plot0

où $\alpha$ est le taux de mortalité induit par le virus (que nous avions négligé jusqu'ici). Le modèle s'écrit : $\begin{eqnarray} \frac{\mathrm{d}S}{\mathrm{d}t}&=&-\beta \frac{I}{N}S\,,\\ \frac{\mathrm{d}I}{\mathrm{d}t}&=&\beta \frac{I}{N}S - (\alpha+\gamma)I\,,\\ \frac{\mathrm{d}R}{\mathrm{d}t}&=&\gamma I\,,\\ \frac{\mathrm{d}D}{\mathrm{d}t}&=&\alpha I\,. \end{eqnarray}$

Modèle d'observation

Nous faisons l'hypothèse que le nombre de décès cumulés observé au jour $t$ est tiré dans une loi de Poisson de moyenne $D(t)$ telle que donné par le modèle : $D_{\small\mbox{data}}(t)\sim \mbox{Poisson}\left(D_{\small\mbox{model}}(t)\right)$ En admettant que les observations sont indépendantes conditionnellement au modèle, la vraisemblance s'écrit : $\mbox{Like}(\theta)=\prod_{t=0}^{T} \mbox{Prob}(\mbox{observe }c(t)|\mbox{ model predicts }p(t))\times \mbox{Prob}(\mbox{observe }D_{\small\mbox{data}}(t)|D_{\small\mbox{model}}(t))\,.$ Soit $\theta = \{ \beta, \kappa, \alpha \}$ le vecteur des paramètres à estimer. Rechercher les valeurs de $\theta$ qui maximisent la vraisemblance est équivalent à rechercher les valeurs de $\theta$ qui maximisent la log-vraisemblance, qui transforme le produit en somme : $\mbox{logLike}(\theta)=\sum_{t=0}^T \log\left(\mbox{Prob}(\mbox{observe }c(t)|\mbox{ model predicts }p(t))\times \mbox{Prob}(\mbox{observe }D_{\small\mbox{data}}(t)|D_{\small\mbox{model}}(t))\right)\,.$ Nous travaillerons avec la log-vraisemblance.

Traitement des données

On importe les données de décès :

# Lien permanent vers les données d'hospitalisations
urlhosp = url("https://www.data.gouv.fr/fr/datasets/r/6fadff46-9efd-4c53-942a-54aca783c30c")

# Tableau lié aux données d'hospitalisations
datahosp = read.csv2(urlhosp, header=TRUE, sep=";")

Agrégation des données à l’échelle de la France (tous les départements français) par jour :

# Nombre de décès par jour
nb_deces = aggregate(incid_dc~ jour, data=datahosp, FUN = sum)

On sélectionne les données du 1er septembre au 31 octobre :

nb_deces  <-filter(nb_deces, jour>= "2020-09-01",jour<= "2020-10-31"  )

Construction du vecteur qui contient uniquement les données de décès :

dc=nb_deces[,2] # Nombre de décès
dccum=cumsum(dc)-dc[1] # Nombre de décès cumulés depuis le 1er septembre 
LD=length(dc)

On représente l’évolution du nombre de patients décédés cumulés dans les hôpitaux depuis le 1er septembre :

plot(1:LD,dccum,xlab="Temps écoulé depuis le 1 septembre (en jours)",ylab="Nombre cumulé de décès",pch=16, col="dark green",main="Evolution du nombre de patients décédés
au cours de la deuxième flambée")

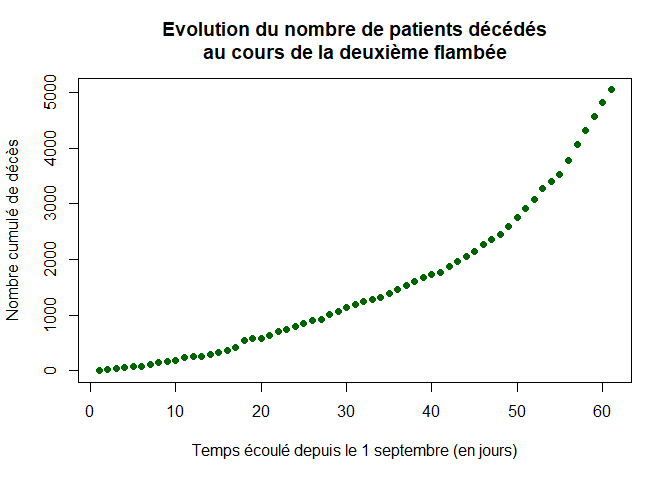
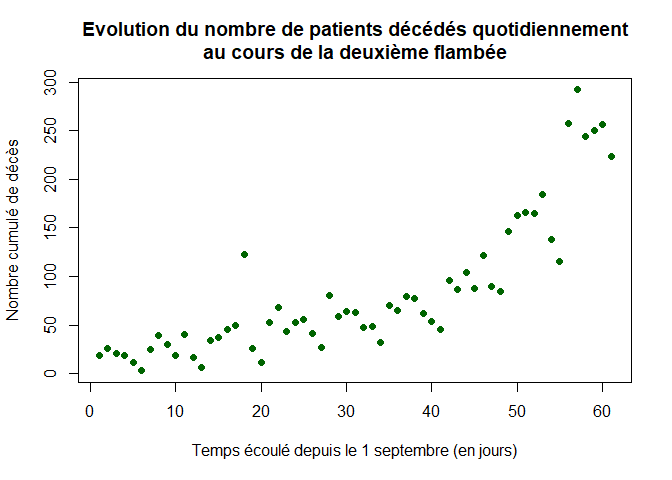
On représente l’évolution du nombre de patients décédés quotidiens dans les hôpitaux au cours de la deuxième flambée :

plot(1:LD,dc,xlab="Temps écoulé depuis le 1 septembre (en jours)",ylab="Nombre cumulé de décès",pch=16, col="dark green",main="Evolution du nombre de patients décédés quotidiennement
au cours de la deuxième flambée")

Ajustement du modèle aux données

On initialise les paramètres du modèle SIRD :

N = 67e6 # Taille de la population française
gamma = 1/10 # Taux de guérison (inverse du temps moyen avant guérison)
R_0 = 3 # Reproductivité du virus
beta = gamma*R_0 # Taux de transmission du virus 
sigma = 0.7 # Sensibilité des tests
kappa = 5e-3 # Biais d'observation
alpha = 0.01 # Taux de mortalité due au virus

theta0 = c(beta,kappa,alpha) # Vecteur des paramètres à estimer (estimations initiales)

On choisit de commencer l'ajustement au 15 septembre pour tenir compte du décalage temporel entre les infections et les décès. On définit les conditions initiales :

t0=15 # On choisit de commencer l'ajustement au 15 septembre
t=t0:LD # Vecteur temps 

I0=100000 # On fixe le nombre initial d'infectés à 100 000 (estimation grossière)
R0=5/100*N # On suppose qu'au 1er avril il y a 5% d'immunisés (estimation grossière)
D0=dccum[t0] # Nombre de décès au 1er septembre
S0=N-I0-R0-D0 # Nombre de personnes susceptibles d'êtres infectées

X0=c(S0,I0,D0) # Vecteur d'état (conditions initiales)

On crée une fonction qui simule le modèle SIRD :

SIRD = function(t, X, P){ 
  beta = P[1] ; alpha = P[2]
  S = X[1] ; I = X[2] ; D = X[3]

  y = beta*S*I/N # Nouvelles infections par unité de temps

  dS = -y
  dI = +y - gamma*I - alpha*I
  dD = +alpha*I
  dX = c(dS,dI,dD)

  return(list(dX))
}

On crée une fonction qui calcule la vraisemblance des paramètres :

logLike = function(theta){
  beta = theta[1]
  kappa = theta[2]
  alpha = theta[3]

  P = c(beta,alpha)

  X = ode(X0,t,SIRD,P) 

  # Proportion théorique de tests quotidiens positifs d'après le modèle 
  p = sigma*X[,3]/(X[,3]+kappa*X[,2])
  dcth = alpha*X[,3] # Décès théoriques 

  LLT = dbinom(PT[t], TT[t], p, log=TRUE) # Pr(observer "PT" test positifs au temps t)
  LLD = dpois(dc[t], dcth, log=TRUE) # Probabilité d'observer "dc" décès au temps t 
  LL = sum(c(LLT,LLD))
  return(LL)
}

On optimise la vraisemblance donnée par la fonction LogLike :

opt = optim(theta0,logLike,control=list(fnscale=-1))

On récupère les paramètres optimaux :

beta = opt$par[1]
kappa = opt$par[2] 
alpha = opt$par[3]
P0 = c(beta,alpha) # Vecteur des paramètres mis à jour

On calcule la solution du modèle pour les paramètres estimés :

X = ode(X0,t,SIRD,P0) 

p=sigma*X[,3]/(X[,3]+kappa*X[,2])

On représente les évolutions du nombre de décès cumulés théoriques (courbe noire) et observés (courbe rouge) :

plot(1:LD,dccum,col="red",xlab="Temps écoulé depuis le 1er septembre (en jours)",ylab="Nombre de décès cumulés",pch=16,main="Evolutions du nombre de décès cumulés théoriques et observés")
lines(t,X[,4])
legend("topleft",legend="Nombre de décès observés",pch=16,col="red",bty="n")
legend(x=-2, y=4700,legend="Nombre de décès théoriques",lty=1,col="black",bty="n")

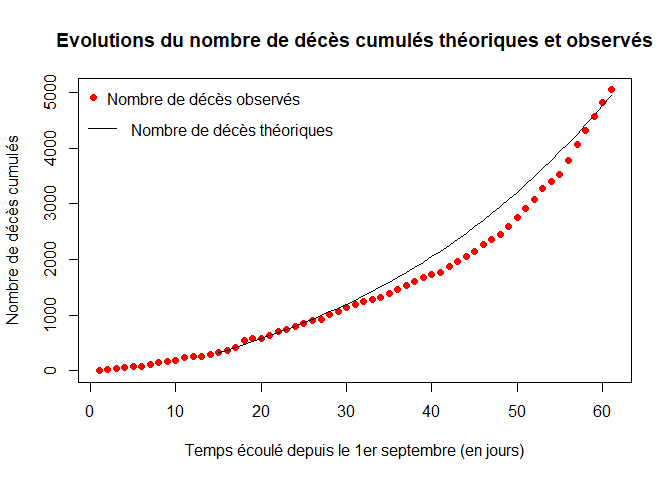
On représente l' évolution du nombre de décès quotidiens théoriques (courbe noire) et observés (courbe rouge).

plot(1:LD,dc,col="red",xlab="Temps écoulé depuis le 1er septembre (en jours)",ylab="Nombre de décès quotidiens",pch=16, main="Evolutions du nombre de décès quotidiens théoriques et observés")
lines(t,alpha*X[,3])
legend("topleft",legend="Nombre de décès quotidiens observés",pch=16,col="red",bty="n")
legend(x=-2, y=280,legend="Nombre de décès quotidiens théoriques",lty=1,col="black",bty="n")

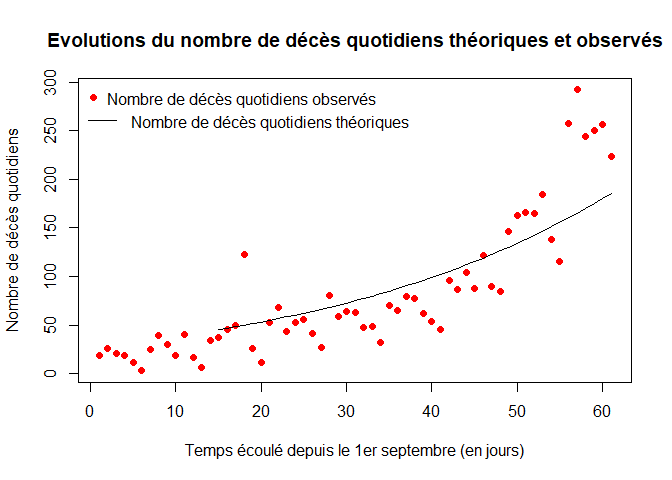
Le modèle ne parvient pas à capturer l'accélération de l'épidémie à partir de la mi-octobre.

On réalise de nouveau un graphe représentant l’évolution de la proportion de tests positifs observés, PP, et de la proportion théorique de tests positifs calculés, p, avec le nouveau modèle SIRD.

plot(t,PP[t],pch=16,col="#A162A6", 
     xlab="Temps écoule depuis le 1er Septembre 2020 (en jours)",
     ylab="Proportion de tests positifs quotidiens",
     main = "Proportions de tests positifs observés et théoriques")
lines(t,p, lwd=2, col="#9CE06F")
legend(15, 0.15, legend=c("Tests positifs observés", "Tests positifs théoriques"),col=c("#A162A6", "#9CE06F"), lty=1, cex = 0.8,lwd=2)

Puis, on compare $\sigma_1$ (somme cumulée des tests positifs observés) avec $\sigma_2$ (somme cumulée des tests positifs observés) obtenues avec le nouveau modèle SIRD. On fait ensuite un graphique des sommes cumulées des tests positifs théoriques du modèle SIRD et observés.

sigma1=cumsum(PT[t])
sigma2=cumsum(TT[t]*p) #nombre total de tests réalisés * proportion de tests positifs théoriques
plot(t,sigma1,pch=16,xlab="Temps écoule depuis le 1er septembre 2020 (en jour)",ylab="Somme cumulée des tests positifs",col="#A162A6", main = "Comparaison des sommes cumulées des tests positifs")
lines(t,sigma2,lwd=2, col = "#9CE06F" )
legend(15, 900000, legend=c("Tests positifs observés", "Tests positifs théoriques"),
       col=c("#A162A6", "#9CE06F"), lty=1, cex = 0.8, lwd=2)

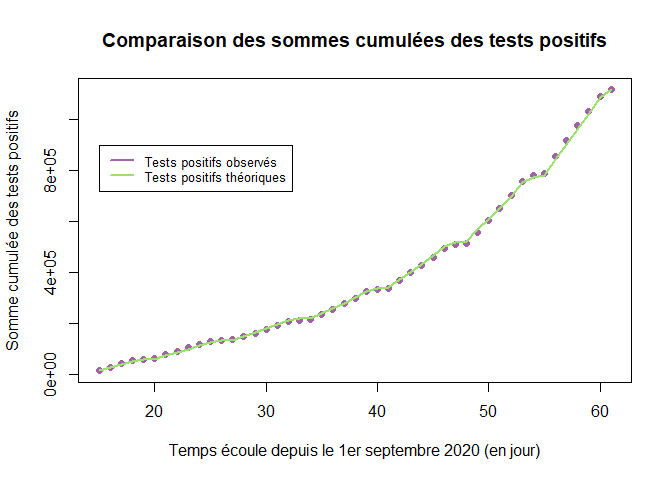
L'ajustement du modèle SIRD est très similaire à celui du modèle SIR en termes de tests.

Estimation de la létalité du virus

A l’aide de nos paramètres estimés, nous sommes en mesure de calculer le nombre de reproduction effectif du virus au cours de la deuxième flambée :

R_e2 = beta/(gamma+alpha)*(S0/N) # Re : nombre de reproduction effectif du virus

print(paste("R_e=",R_e2))

On retrouve une reproductivité $\mathcal R_e \approx 1.3$ .

Nous pouvons également estimer le taux de létalité (IFR) du virus durant la 2eme flambée :

IFR = alpha/(alpha+gamma) # Infection Fatality Ratio

print(paste("IFR=",IFR))

Nous trouvons un IFR de 0.45%, comparable à celui estimé lors de la première flambée.

Keys	Action
`?`	Open this help
`n`	Next page
`p`	Previous page
`s`	Search